|
 |
|
 |
| EN |
|
Поиск по сайту
Авторизация
Подписка на новости
|
Закон сохранения заряда
Зако́н сохране́ния электри́ческого заря́да гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется.
Закон сохранения заряда выполняется абсолютно точно. На данный момент его происхождение объясняют следствием принципа калибровочной инвариантности. Требование релятивистской инвариантности приводит к тому, что закон сохранения заряда имеет локальный характер: изменение заряда в любом наперёд заданном объёме равно потоку заряда через его границу. В изначальной формулировке был бы возможен следующий процесс: заряд исчезает в одной точке пространства и мгновенно возникает в другой. Однако такой процесс был бы релятивистски неинвариантен: из-за относительности одновременности в некоторых системах отсчёта заряд появился бы в новом месте до того, как исчез в предыдущем, а в некоторых — заряд появился бы в новом месте спустя некоторое время после исчезновения в предыдущем. То есть был бы отрезок времени, в течение которого заряд не сохраняется. Требование локальности позволяет записать закон сохранения заряда в дифференциальной и интегральной форме. Закон сохранения заряда и калибровочная инвариантность
Физическая теория утверждает, что каждый закон сохранения основан на соответствующем фундаментальном принципе симметрии. Со свойствами симметрий пространства-времени связаны законы сохранения энергии, импульса и момента импульса. Законы сохранения электрического, барионного и лептонного зарядов связаны не со свойствами пространства-времени, а с симметрией физических законов относительно фазовых преобразований в абстрактном пространстве квантовомеханических операторов и векторов состояний. Заряженные поля в квантовой теории поля описываются комплексной волновой функцией Закон сохранения заряда в интегральной формеВспомним, что плотность потока электрического заряда есть просто плотность тока. Тот факт, что изменение заряда в объёме равно полному току через поверхность, можно записать в математической форме:
Здесь Закон сохранения заряда в дифференциальной формеПереходя к бесконечно малому объёму и используя по мере необходимости теорему Стокса можно переписать закон сохранения заряда в локальной дифференциальной форме (уравнение непрерывности)
Закон сохранения заряда в электроникеПравила Кирхгофа для токов напрямую следуют из закона сохранения заряда. Объединение проводников и радиоэлектронных компонентов представляется в виде незамкнутой системы. Суммарный приток зарядов в данную систему равен суммарному выходу зарядов из системы. В правилах Кирхгофа предполагается, что электронная система не может значительно изменять свой суммарный заряд. Экспериментальная проверкаНаилучшей экспериментальной проверкой закона сохранения электрического заряда является поиск таких распадов элементарных частиц, которые были бы разрешены в случае нестрогого сохранения заряда. Такие распады никогда не наблюдались.Лучшее экспериментальное ограничение на вероятность нарушения закона сохранения электрического заряда получено из поиска фотона с энергией mec2/2 ≈ 255 кэВ, возникающего в гипотетическом распаде электрона на нейтрино и фотон:
однако существуют теоретические аргументы в пользу того, что такой однофотонный распад не может происходить даже в случае, если заряд не сохраняется. Другой необычный несохраняющий заряд процесс — спонтанное превращение электрона в позитрон и исчезновение заряда (переход в дополнительные измерения, туннелирование с браны и т. п.). Наилучшие экспериментальные ограничения на исчезновение электрона вместе с электрическим зарядом и на бета-распад нейтрона без эмиссии электрона:
Источник: ru.wikipedia.org |
Читайте бесплатно
События из истории измерений
| ||||||||||||||||||||||||||||||||||||||
























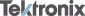




 , где x — пространственно-временная координата. Частицам с противоположными зарядами соответствуют функции поля, различающиеся знаком фазы
, где x — пространственно-временная координата. Частицам с противоположными зарядами соответствуют функции поля, различающиеся знаком фазы  , которую можно считать угловой координатой в некотором фиктивном двумерном «зарядовом пространстве». Закон сохранения заряда является следствием инвариантности лагранжиана относительно глобального калибровочного преобразования типа
, которую можно считать угловой координатой в некотором фиктивном двумерном «зарядовом пространстве». Закон сохранения заряда является следствием инвариантности лагранжиана относительно глобального калибровочного преобразования типа  , где Q — заряд частицы, описываемой полем
, где Q — заряд частицы, описываемой полем  , а
, а  — произвольное вещественное число, являющееся параметром и не зависящее от пространственно-временных координат частицы. Такие преобразования не меняют модуля функции, поэтому они называются унитарными U(1).
— произвольное вещественное число, являющееся параметром и не зависящее от пространственно-временных координат частицы. Такие преобразования не меняют модуля функции, поэтому они называются унитарными U(1).

 — некоторая произвольная область в трёхмерном пространстве,
— некоторая произвольная область в трёхмерном пространстве, 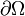 — граница этой области,
— граница этой области,  — плотность заряда,
— плотность заряда,  — плотность тока (плотность потока электрического заряда) через границу.
— плотность тока (плотность потока электрического заряда) через границу.