Теорема Котельникова

О выборе числа отсчетов и восстановлении сигналов

Принципиально важным теоретически и практически является вопрос о выборе числа отсчетов сигнала для его преобразования в цифровую форму и дальнейшего восстановления сигнала по его отсчетам. Как часто надо делать равномерные выборки произвольного сигнала, чтобы после преобразования в цифровую форму, а затем снова в аналоговую была сохранена форма сигнала? Ответ на этот важный вопрос дает теорема об отсчетах или теорема Котельникова (за рубежом именуемая также теоремой Найквиста, теоремой об отсчетах и т.д.): «Если спектр сигнала e(t) ограничен высшей частотой f_В, то он без потери информации может быть представлен дискретными отсчетами с числом, равным 2×f_В». При этом сигнал восстанавливается по его отсчетам e(k×dt), следующим с интервалом времени dt=1/f_В, с помощью фильтра, реализующего восстановление по формуле:

(1)

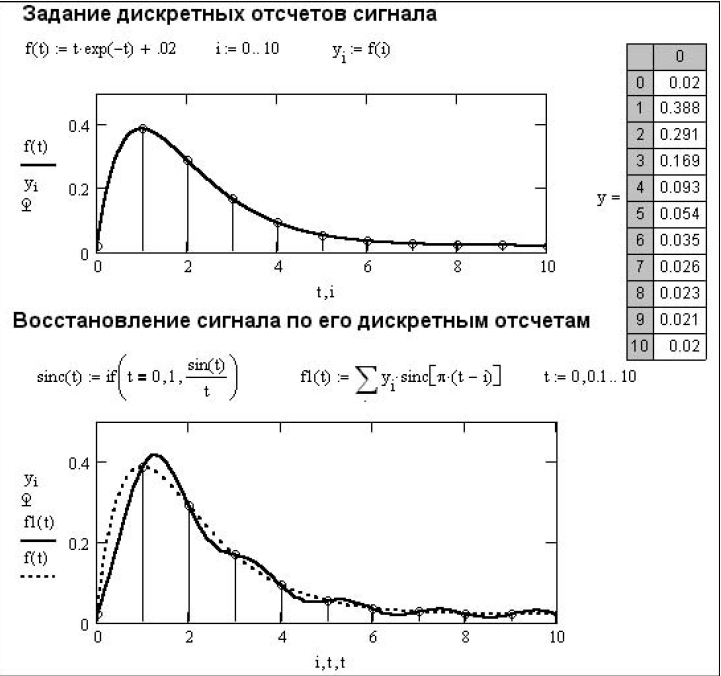
Для восстановления непрерывного сигнала по его выборкам достаточно располагать функцией sinc(t)=sin(t)/t с учетом ее особого значения sinc(t)=1 при x=0. Рисунок показывает пример дискретизации некоторого сигнала (нарастающая, а затем спадающая экспоненты) с периодом квантования dt и затем восстановления сигнала по выражению (1). Несмотря на малое число отсчетов (их 11) восстановленная форма сигнала весьма близка к форме исходного сигнала.

Демонстрация дискретизации и восстановления сигнала в системе компьютерной математики Mathcad

Чтобы восстановить исходный сигнал по его отсчетам надо иметь численные значения их и значение интервала дискретизации dt. Все эти данные нетрудно хранить в запоминающем устройстве. Если увеличить dt при восстановлении сигнала по формуле (5.1) в k раз, то восстановленный сигнал без изменения формы будет растянут в k раз и его можно отобразить на экране достаточно низкочастотной ЭЛТ с простым низкочастотным усилителем.

Для восстановления сигнала не обязательно пользоваться фильтром на основе базиса Котельникова. Возможно применение и более простых фильтров, вплоть до обычного конденсатора или RC-фильтров нижних частот. Правда, при этом нужно несколько увеличивать частоту выборок.