 |
 |
|
 |
| EN |
|
Поиск по сайту
Авторизация
Подписка на новости
|
Закон Ома
Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году и назван в честь его первооткрывателя Георга Ома.
В своей оригинальной форме он был записан его автором в виде :
Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и независящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) В таком случае в современных терминах, и в соответствии с предложенной автором записью, формулировка Ома (1) выражает Закон Ома для полной цепи:
где:
Из закона Ома для полной цепи вытекают следствия:
Часто выражение:
(где Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:
То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС. К другой записи формулы (3), а именно:
Применима другая формулировка: Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи. Выражение (5) можно переписать в виде:
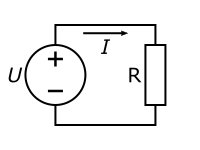
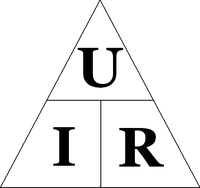
где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо, впоследствии переименованный в Си́менс (обозначение: См, S). Мнемоническая диаграмма для Закона
В соответствии с этой диаграммой формально может быть записано выражение:
Которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно. В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:
где:
Закон Ома и ЛЭП
Одним из важнейших требований к линиям электропередачи (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока В таком случае потери мощности будут определяться выражением:
Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако, для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее, практически используемое, напряжение в дальних ЛЭП не превышает миллиона вольт. Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём, излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение. Закон Ома в дифференциальной форме
Сопротивление Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем: где:
Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1). Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред. Закон Ома для переменного токаВышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига.
Если ток является синусоидальным с циклической частотой
где:
При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо. Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и от сопротивления и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда. Трактовка закона ОмаЗакон Ома можно просто объяснить при помощи теории Друде:
Здесь:
Источник: ru.wikipedia.org Материалы по теме:
Новости КИПиС
Новости компаний
Энциклопедия измерений
Статьи КИПиС
|
Читайте бесплатно
События из истории измерений
|




























 ,
,
 , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r.
, l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r.
 , (2)
, (2)
 — ЭДС источника напряжения(В),
— ЭДС источника напряжения(В), — сила тока в цепи (А),
— сила тока в цепи (А), — сопротивление всех внешних элементов цепи (Ом),
— сопротивление всех внешних элементов цепи (Ом), — внутреннее сопротивление источника напряжения (Ом).
— внутреннее сопротивление источника напряжения (Ом).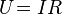 (3)
(3)
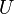 есть напряжение или падение напряжения или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».
есть напряжение или падение напряжения или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».
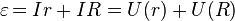 (4)
(4)
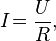 (5)
(5)
 (6)
(6)
 (7)
(7)
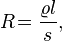 (8)
(8)
 — удельное сопротивление материала, из которого сделан проводник,
— удельное сопротивление материала, из которого сделан проводник, — его длина
— его длина — площадь его поперечного сечения
— площадь его поперечного сечения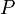 =
= 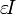 при минимальных потерях мощности в линии передачи
при минимальных потерях мощности в линии передачи 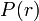 =
= 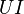 , где
, где  , причём
, причём  (9)
(9)

 — вектор плотности тока,
— вектор плотности тока,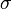 — удельная проводимость,
— удельная проводимость, — вектор напряжённости электрического поля.
— вектор напряжённости электрического поля. , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:
, а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:

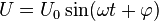 подбором такой
подбором такой  что
что  Тогда все значения токов и напряжений в схеме надо считать как
Тогда все значения токов и напряжений в схеме надо считать как 

 — электрическая удельная проводимость
— электрическая удельная проводимость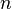 — концентрация электронов
— концентрация электронов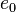 — элементарный заряд
— элементарный заряд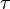 — время релаксации по импульсам (время, за которое электрон «забывает» о том в какую сторону двигался)
— время релаксации по импульсам (время, за которое электрон «забывает» о том в какую сторону двигался) — эффективная масса электрона
— эффективная масса электрона

