 |
 |
|
 |
| EN |
|
Поиск по сайту
Авторизация
Подписка на новости
|
Закон всемирного тяготения
Класси́ческая тео́рия тяготе́ния Ньюто́на (Зако́н всео́бщего тяготе́ния Ньюто́на) — закон, описывающий гравитационное взаимодействие в рамках классической механики. Этот закон был открыт Ньютоном в 1666 году. Он гласит, что сила гравитационного притяжения между двумя материальными точками массы 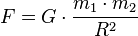
Здесь Свойства ньютоновского тяготения
Исторический очерк
Закон тяготения Ньютона
Сама идея всеобщей силы тяготения неоднократно высказывалась и до Ньютона. Ранее о ней размышляли Эпикур, Гассенди, Кеплер, Борелли, Декарт, Роберваль, Гюйгенс и другие. Кеплер полагал, что тяготение обратно пропорционально расстоянию до Солнца и распространяется только в плоскости эклиптики; Декарт считал его результатом вихрей в эфире. Были, впрочем, догадки с правильной зависимостью от расстояния; Ньютон в письме к Галлею упоминает как своих предшественников Буллиальда, Рена и Гука. Но до Ньютона никто не сумел ясно и математически доказательно связать закон тяготения (силу, обратно пропорциональную квадрату расстояния) и законы движения планет (законы Кеплера). В своём основном труде «Математические начала натуральной философии» (1687) Исаак Ньютон вывел закон тяготения, основываясь на эмпирических законах Кеплера, известных к тому времени. Он показал, что:
Теория Ньютона, в отличие от гипотез предшественников, имела ряд существенных отличий. Ньютон опубликовал не просто предполагаемую формулу закона всемирного тяготения, но фактически предложил целостную математическую модель:
В совокупности эта триада достаточна для полного исследования самых сложных движений небесных тел, тем самым создавая основы небесной механики. До Эйнштейна никаких принципиальных поправок к указанной модели не понадобилось, хотя математический аппарат оказалось необходимым значительно развить. Отметим, что теория тяготения Ньютона уже не была, строго говоря, гелиоцентрической. Уже в задаче двух тел планета вращается не вокруг Солнца, а вокруг общего центра тяжести, так как не только Солнце притягивает планету, но и планета притягивает Солнце. Наконец, выяснилась необходимость учесть влияние планет друг на друга. Со временем оказалось, что закон всемирного тяготения позволяет с огромной точностью объяснить и предсказать движения небесных тел, и он стал рассматриваться как фундаментальный. В то же время ньютоновская теория содержала ряд трудностей. Главная из них — необъяснимое дальнодействие: сила притяжения передавалась непонятно как через совершенно пустое пространство, причём бесконечно быстро. По существу ньютоновская модель была чисто математической, без какого-либо физического содержания. Кроме того, если Вселенная, как тогда предполагали, евклидова и бесконечна, и при этом средняя плотность вещества в ней ненулевая, то возникает гравитационный парадокс. В конце XIX века обнаружилась ещё одна проблема: расхождение теоретического и наблюдаемого смещения перигелия Меркурия. Дальнейшее развитиеОбщая теория относительностиНа протяжении более двухсот лет после Ньютона физики предлагали различные пути усовершенствования ньютоновской теории тяготения. Эти усилия увенчались успехом в 1915 году, с созданием общей теории относительности Эйнштейна, в которой все указанные трудности были преодолены. Теория Ньютона, в полном согласии с принципом соответствия, оказалась приближением более общей теории, применимым при выполнении двух условий:
Квантовая гравитацияОднако и общая теория относительности не является окончательной теорией гравитации, так как неудовлетворительно описывает гравитационные процессы в квантовых масштабах (на расстояниях порядка планковского, около 1,6·10−35 м). Источник: ru.wikipedia.org |
Читайте бесплатно
События из истории измерений
|




























 и
и 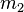 , разделёнными расстоянием
, разделёнными расстоянием  , пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:
, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть: — гравитационная постоянная, равная
— гравитационная постоянная, равная 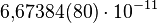 м³/(кг с²).
м³/(кг с²). определяется формулой:
определяется формулой:
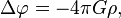

 , связана с потенциалом формулой:
, связана с потенциалом формулой:
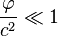 .
.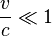 .
.
